地理信息系統可以將不同尺度、不同系統的地圖相結合后,進行迭圖空間分析。為了將這些不同尺度與系統的圖資迭合在一起,必須有一個彼此間運算處理之共同框架,此即為投影及坐標系統。本文介紹的是投影。
理解投影需要一些地圖學的內容,如有需要可以參考:《地圖學》課程整理匯總
地圖是將地球上的自然現象和社會現象通過概括和符號縮繪在平面上的圖形,這些信息便成為 GIS 數據分析的重要來源。由于地圖是平面的,將把地球球面上的信息描繪到平面上時,平面與球面的矛盾就產生了。例如大范圍的地區,強行將球面數據變成平面,會產生斷裂或重迭的情形,如此就不能獲得完整與連續的地表數據。為了解決這個問題,于是科學家透過不同的地圖投影來解決這個問題。
所謂投影(Projection)就是透過一些數學法則,將地球球面的位置轉成平面位置,并建立起相對應的經緯柵格。在轉成平面的過程中,會有部分地區發生變形的情形,需視情況選擇變形最小的投影方法。
按變形特性劃分
正形投影(conformal projection)
保持原來地物的角度不變,目的確保形狀不受扭曲變形,缺點是面積在投影過程中,會造成扭曲。如蘭柏特(Lambert)圓錐投影及麥卡托(Mercator)圓柱投影。
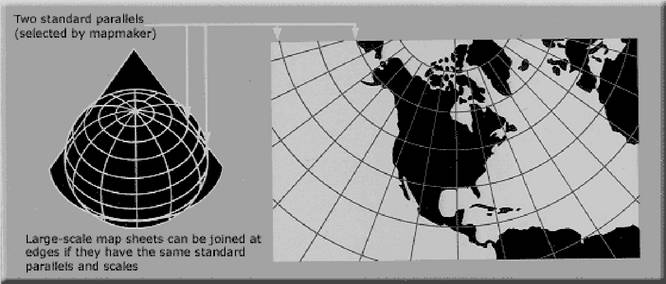
圖:蘭柏特圓錐投影圖

圖:麥卡托圓柱投影圖
等積投影(equivalent projection)
確保投影前后之區域面積不變,但形狀、角度、比例都可能會扭曲。如穆爾威(Mollweid)投影、彭納(Bonne)投影、正弦(Sinusoidal)等積投影。
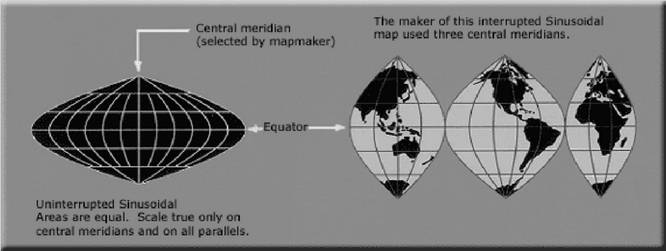
圖:正弦等積投影圖
等距投影(Equidistanct projection)
投影前后兩地之前的距離不變。如圓錐投影。
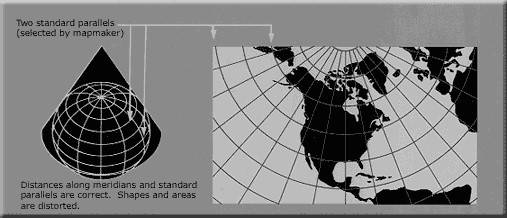
圖:蘭柏特等距圓錐投影圖
等角投影(Azimuthal projection)
投影前后兩點的方位角(夾角)保持不變,代表與球面上所量得的方位一致,而且依據此投影方式所得地圖上兩點之直線距離并非為最短距離。例如地圖上的飛行航線,大圓航線才是最短距離。許多的等角投影也會是等形(如Mercator 投影)、等面積或等距離投影。
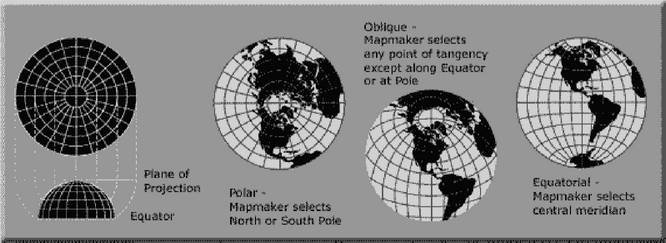
圖 : 等角等距投影圖
依投影面與地球接觸位置分
圓錐投影(Conical projection)
將地球球面投影至與之相切或相割的圓錐面,再展開成平面。通常在球面與圓椎面相交的地方附近的面積最準確,屬于等距離投影。

圖 :圓錐投影圖
圓柱投影(Cylindrical projection)
地球球面投影在圓柱筒上,在將圓柱加以展開,地球球面與圓柱相交的地方是一個大圓,通常是赤道。投影出的地圖的經線和緯線和原本地球儀上的一樣,互相垂直。屬于一種正形投影。

圖 :圓柱投影圖
方位投影(Azimuthal projection)
又稱平面投影,將地球球面與投影平面相切或相割,依照光源位置可分為正射與中心投影。投影出來的平面地圖呈圓形,緯線為同心圓,經線則從圓心向外作放射線。這種投影法所投影出來的地圖面積比例和實際相符。

圖:方位投影圖













