概述:
**
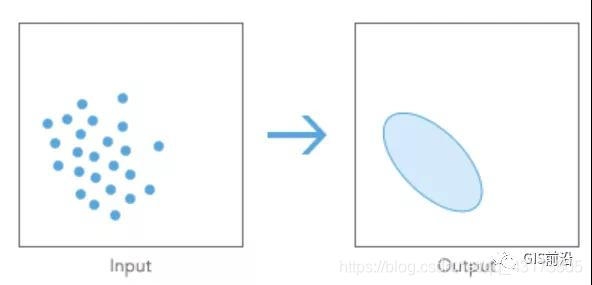
創建標準差橢圓來匯總地理要素的空間特征:中心趨勢、離散和方向趨勢。

公式:
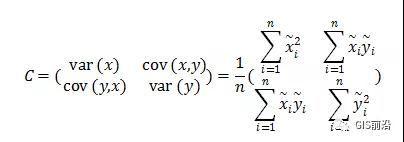
說明:
1、輸出:
標準差橢圓工具可創建一個其中每個案例(案例分組字段參數)都對應一個橢圓面的新的輸出要素類。這些橢圓面的屬性值會包括平均中心的 X 和 Y 坐標、兩個標準距離(長軸和短軸)及橢圓的方向。字段名分別是 CenterX、CenterY、XStdDist、YStdDist 和 Rotation。如果提供了案例分組字段,那么也會將此字段添加到輸出要素類。
2、注意事項:
基于歐氏距離或者曼哈頓距離的計算需要對數據進行投影以準確測量距離。至于歐氏距離和曼哈頓距離是什么,在這里做簡單的解釋:
①歐氏距離: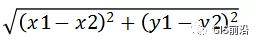
②曼哈頓距離: 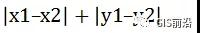
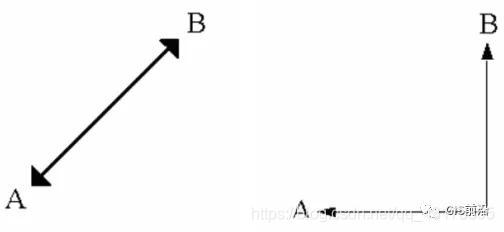
上面兩張圖很清晰的表示了歐式距離與曼哈頓距離的區別,左圖即表示歐氏距離,也就是兩點之間的直線距離,右圖表示了曼哈頓距離,兩點的垂直距離。曼哈頓距離何時用?如果你想要開車從B點到A點,但是道路限制為僅南北行駛和東西行駛,那么此時B到A的距離就是你需要采用曼哈頓距離來計算啦!當然如果你有直升機,那么就可以采用歐氏距離計算了!
**
試驗:
**
我們以粵港澳大灣區為例,以密密麻麻的交通信號燈點數據為分析數據,數據源來自OSM:
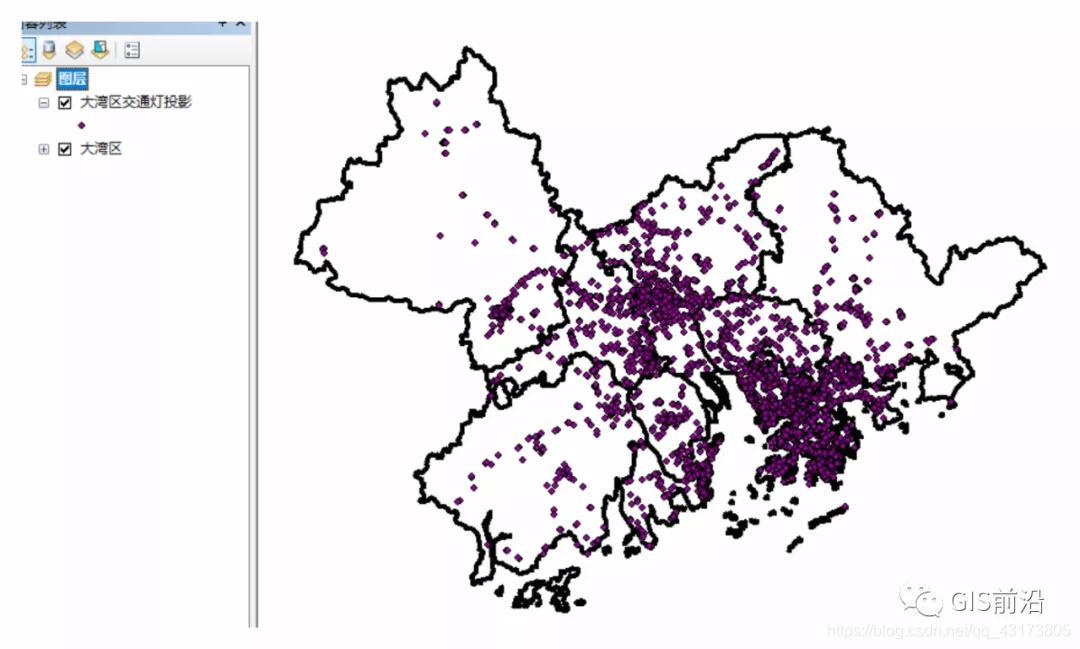
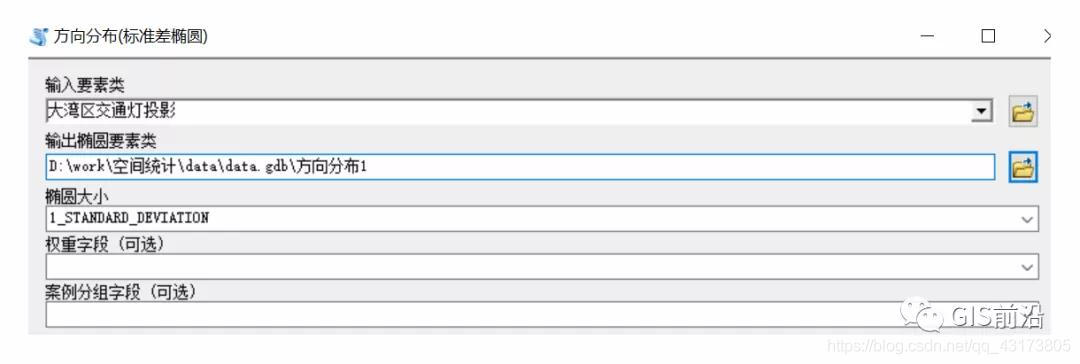
在Spatial Statistics Tools中的度量地理分布-方向分布(標準差橢圓)可以找到:

實際上這個工具的參數也是比較少,并且跟標準距離的選擇差不多,標準距離中有一個圓大小,可以選擇1/2/3個標準差大小的圓,那么方向分布也是同樣,可以選擇1/2/3個標準差距離的橢圓,同樣是會包括63%、98%、99%的要素。
我們先采用默認的一個標準距離觀察結果:
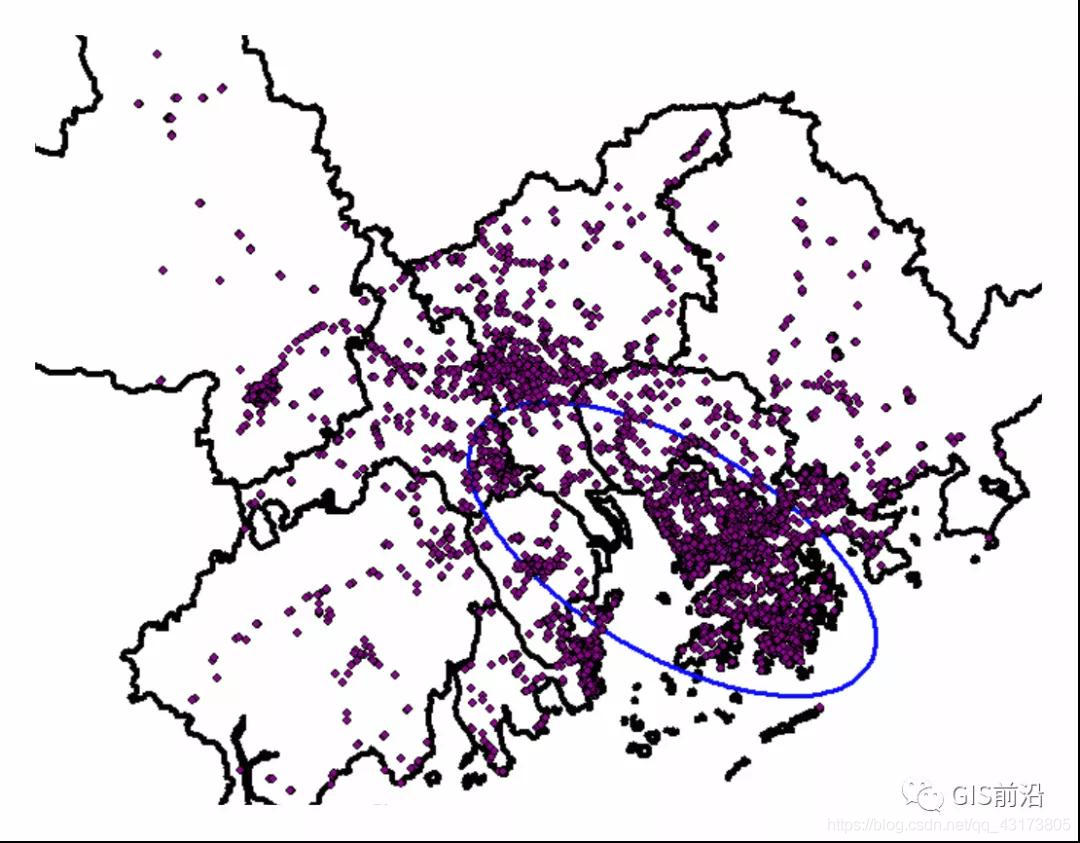
我們可以發現,似乎這次生成的橢圓的圓心與上次的標準距離圓的圓心在同一位置,恭喜你,眼神不錯!在生成的屬性表匯總觀察,圓心的XY坐標是沒有變化的,也就是說,我們采用標準距離橢圓與標準距離圓生成的圓心是在同一個地點的,XStdDist、YStdDist其實就是標準距離的長軸與標準距離的短軸之長度,Rotation代表著長軸順時針開始測量的旋轉的角度。
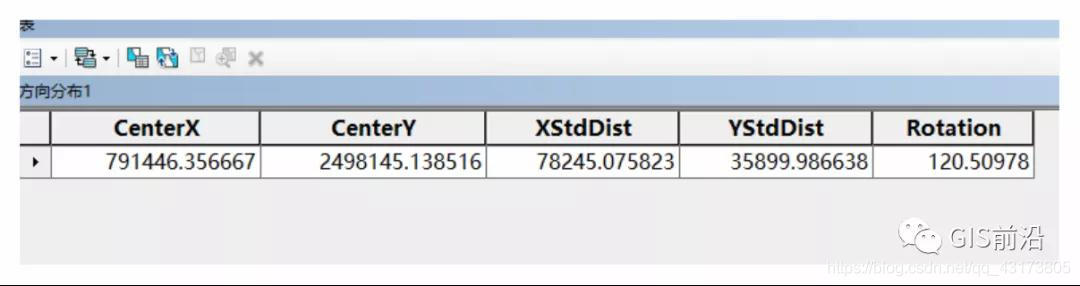
我們再采用兩個標準距離橢圓來觀察: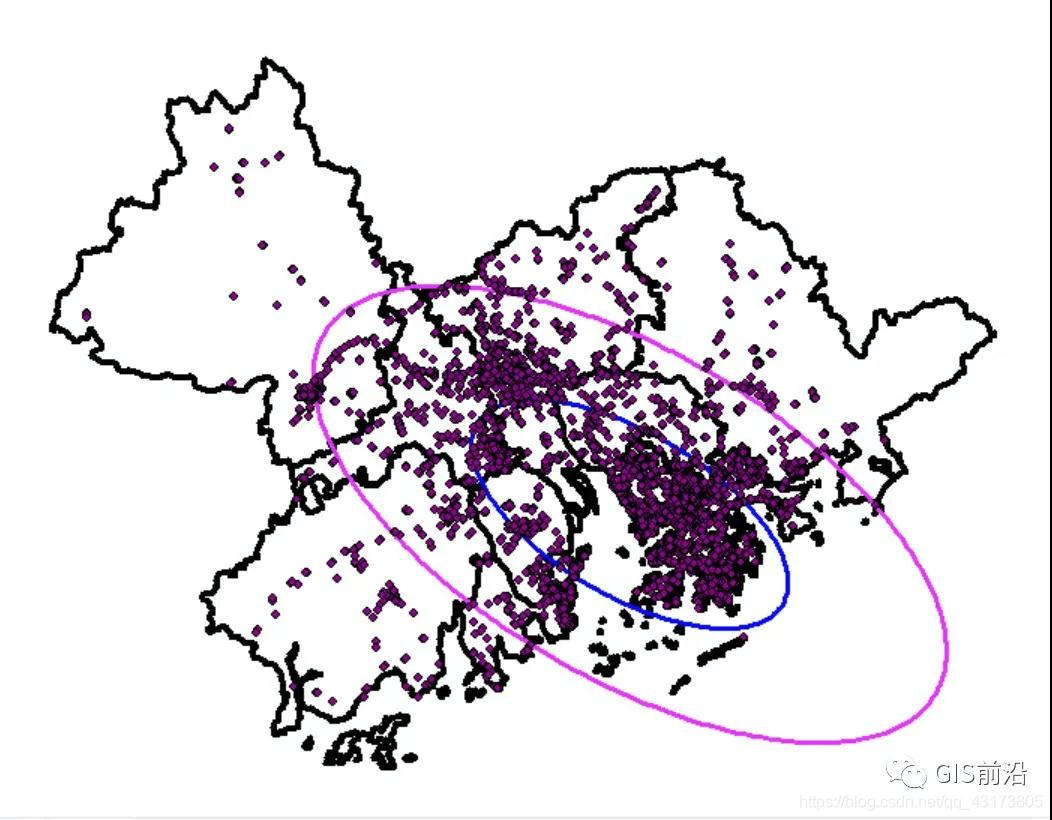
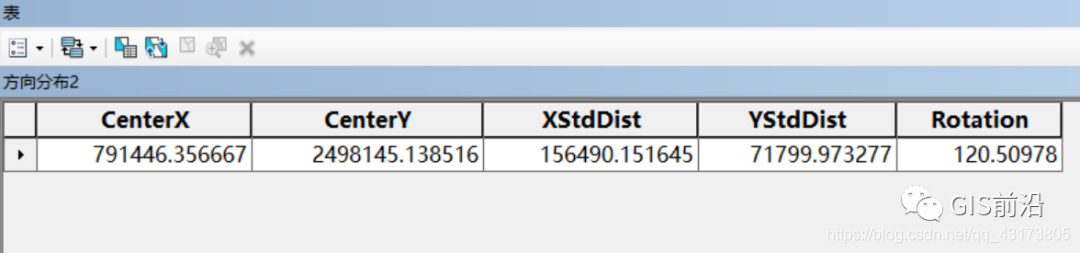
細心的觀眾已經發現了,圓心的XY坐標是永遠不會變的,XStdDist、YStdDist就是兩倍的標準距離的長軸與標準距離的短軸之長度,而Rotation也是不會變的,此時觀眾老爺們又要發問了:這到底與上次的標準距離有什么區別??
其實要我說,建議大家采用標準橢圓分布,而不采用標準圓分布,因為這個不但可以告訴你圓心的位置,還可以告訴你方向呀!我們可以很明顯的看到,大灣區的交通燈集聚的區域是深圳-香港沒錯,但是方向呢?是廣州-深圳-香港方向延伸的,也就是大致呈西北-東南分布,那么此時,我們就可以根據這個結果進行描述:“在XXX°E,XXX°N,以XXX米為長半軸、XXX米為短半軸的橢圓可以囊括大灣區約98%的交通燈,并且交通燈的集聚區域大致呈西北-東南分布,覆蓋廣州、深圳、東莞、香港的絕大部分區域…”這句話放在我們的報告或者論文里,是比僅僅說中心在哪個位置是更好的!
本文鏈接:http://www.aiquka.com/blog/134.html
本文標簽:ArcGIS













