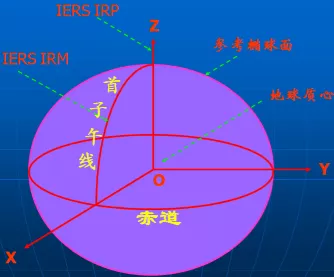
Z軸:由原點指向歷元2000.0的地球參考極的方向;X軸:由原點指向格林尼治參考子午線與赤道面(歷元2000.0)的交點;2000國家大地坐標系采用橢球簡稱CGCS2000橢球。CGCS2000橢球參數
長半軸 α=6378137m
扁率 ?=1/298.257222101
地心引力常數 GM=3.986004418x1014m3s-2地球自轉角速度 ω=7.292115x10-5rads-1 a)CGCS2000參考橢球是一旋轉橢球,其幾何中心與CGCS2000的原點重合,旋轉軸與CGCS2000的Z軸一致,其表面代表地球的數學表面。b)CGCS2000參考橢球又是其表面為正常重力場的等位面的正常橢球。c)CGCS2000參考橢球由四個常數(a,GM,J2,ω)定義。a)“2000中國大地坐標系”,又稱“2000 國家大地坐標系”;英譯為 China Geodetic Coordinate System 2000,縮寫為 CGCS2000;b)CGCS2000由原點、尺度、坐標軸的定向及其時間演變定義,由地面點集合的坐標和速度實現;c) 采用CGCS2000參考橢球參數進行三維坐標變換;d) 大地經緯度變換為地圖平面坐標,采用高斯-克呂格投影或墨卡托投影。2
大地測量控制點坐標轉換技術規范
本標準規定了大地測量控制點坐標轉換到2000國家大地坐標系的技術要求,包括重合點選取、坐標轉換模型、轉換方法、精度評價等。本標準適用于地方獨立坐標系、1954年北京坐標系、1980西安坐標系、WGS-84坐標系以及ITRF框架下的大地測量控制點向2000國家大地坐標系的坐標轉換。2000國家大地坐標系控制點實現精度及省、市級衛星大地控制網C級點、D級點轉換后的精度要求見表1。
2000國家大地坐標系的框架由2000國家大地控制網點組成,其參考框架是ITRF97,參考歷元為2000.0。① 2000國家GPS大地控制網,及其控制下完成的省(市)GPS 基礎控制網;② 在2000系下完成天文大地網聯合平差獲得的近5萬個一、二等天文大地網點;③ 在2000系下平差后獲得的近8萬個三、四等天文大地網點。(2)2000國家大地控制網按精度不同可劃分為三個層次網第一層次為CGCS2000連續運行GPS網(國家CORS系統)。CGCS2000的維持 主要依靠連續運行GPS觀測站, 它們是CGCS2000的骨架, 其坐標精度為mm級, 速度精度為1mm/a。 第二層次為2000國家GPS大地控制網。由全國GPS一、二級網、國家GPS A、 B級網,地殼運動監測網和地殼運動觀測網絡工程網組成, 共計2600多點, 其三維地心坐標精度約為3cm。在2000國家GPS大地控制網下建立的省(市)GPS 基礎控制網。 第三層次為2000系下獲得的全國天文大地控制網(約有5萬點)與全國三、 四等三角網(約有8萬點)。它是CGCS2000的加密框架。全國天文大地網平均點位精度達到±0.11m(整體平差結果),大地高誤差不超過0.5m,全國三、 四等三角網平均點位精度為±0.07m(相對國家一二等三角點分區平差結果)。空間大地網——2000國家GPS大地控制網(20年);2000GPS網2500多點、4600多條基線;當前4508點。天文大地網近5萬點、未知參數20多萬個;30多萬條觀測信息。a)國家級衛星導航定位基準站點:可作為省級及以下衛星導航定位基準站網建設的控制點。b)2000國家GPS大地控制網點:可作為天文大地點控制點及相 對獨立的平面坐標系建立控制點。c)省級衛星導航定位基準站點:點位坐標歸算到2000國家大 地坐標系后,可作為C、D控制點及相對獨立的平面坐標系建立控制點。d)省、市衛星大地控制網C級點、D級點:點位坐標歸算到 2000國家大地坐標系后,可作為建立相對獨立的平面坐標系的控制點。4
模型選用和適用范圍
控制點轉換到2000國家大地坐標系的轉換模型及適用范圍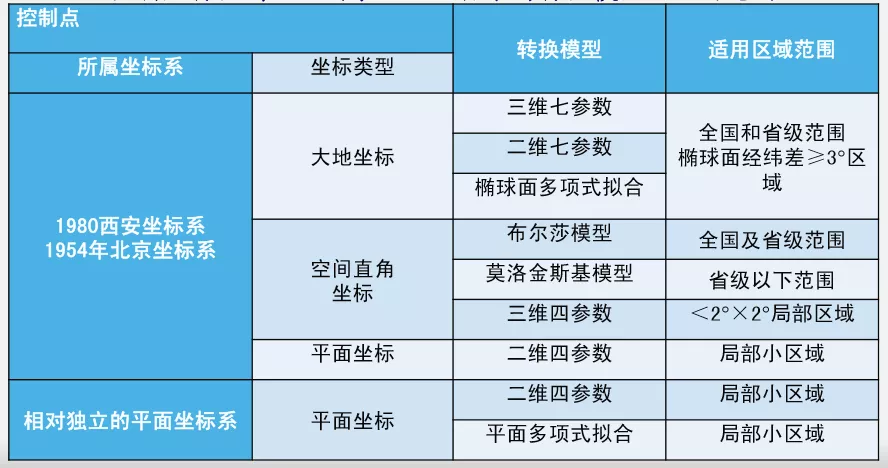
a)空間直角坐標轉換模型:包括布爾莎模型和莫洛金斯基模型,用于不同參考橢球間空間直角坐標轉換,重合點坐標為X、Y和 Z;b)三維七參數大地坐標轉換模型:用于不同參考橢球間的大地坐標轉換,重合點坐標為B、L和H;c)二維七參數大地坐標轉換模型:用于不同參考橢球間的橢球面上大地坐標轉換,重合點坐標為B和L;d)三維四參數空間直角坐標轉換模型:用于不同參考橢球間的空間直角坐標系間的坐標轉換,重合點坐標為X、Y和Z;e)二維四參數平面坐標轉換模型:用于不同高斯投影平面坐標轉換,重合點坐標為x和y;不同坐標系之間的坐標轉換通常有兩類轉換模式:二維轉換模式、三維轉換模式。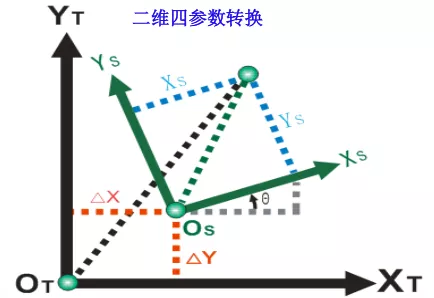

各種轉換模型各有其特點和適用性,因此,在坐標轉換時,對各種坐標轉換模型的適用特點、影響因素及轉換精度進行分析,為不同區域坐標系之間的坐標轉換選擇合適的坐標轉換模型提供依據是十分必要的。


① 布爾莎Bursa七參數為三維空間直角坐標轉換模型,不存在模型誤差和投影變形誤差,可適用于任何區域的高精度坐標轉換。② 二維四參數為高斯平面坐標轉換模型,由于受投影變形誤差的影響,離中央子午線越遠其轉換精度越差,因此,它一般適用于較小區域的轉換。③ 二維七參數為橢球面上的二維轉換模型,不存在投影變形誤差, 因此基本不受范圍的限制,且轉換精度較高。但是它計算復雜。④ 三維多項式與二維多項式均是一種多項式逼近(擬合)的轉換模型。當重合點分布均勻、數量足夠,且目標坐標系的精度比源坐標系的精度高時,可以得到較高的轉換精度。但當重合點數量較少且分布不均勻時,轉換精度降低,尤其不適用于轉換外推。